 are related to one another via a neighborhood system.
A neighborhood system for
are related to one another via a neighborhood system.
A neighborhood system for 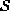 is defined
as
is defined
as
1.2.1
The sites in  are related to one another via a neighborhood system.
A neighborhood system for
are related to one another via a neighborhood system.
A neighborhood system for 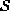 is defined
as
is defined
as
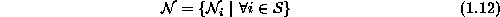
where 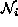 is the set of sites neighboring i. The neighboring
relationship has the following properties:
is the set of sites neighboring i. The neighboring
relationship has the following properties:
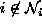 ;
;
 .
.
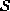 , the neighboring set of i is defined as the
set of nearby sites within a radius of r
, the neighboring set of i is defined as the
set of nearby sites within a radius of r
where 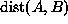 denotes the Euclidean distance between A and
B and r takes an integer value. Note that sites at or near the
boundaries have fewer neighbors.
denotes the Euclidean distance between A and
B and r takes an integer value. Note that sites at or near the
boundaries have fewer neighbors.
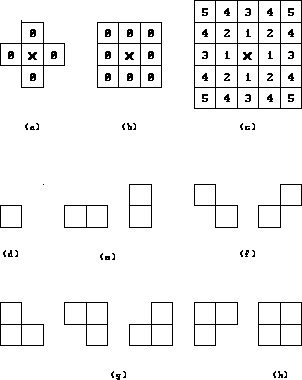
Figure 1.2: Neighborhood and cliques on a lattice of regular sites.
In the first order neighborhood system, also called the 4-neighborhood
system, every (interior) site has four neighbors, as
shown in Fig.1.2(a) where x denotes the considered
site and 0's its neighbors. In the second order neighborhood system,
also called the 8-neighborhood system, there are eight neighbors for every (interior)
site, as shown in Fig.1.2(b). The numbers
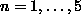 shown in Fig.1.2(c) indicate the
outermost neighboring sites in the n-th order neighborhood system.
The shape of a neighbor set
may be described as the hull enclosing all
the sites in the set.
shown in Fig.1.2(c) indicate the
outermost neighboring sites in the n-th order neighborhood system.
The shape of a neighbor set
may be described as the hull enclosing all
the sites in the set.
When the ordering of the elements in  is specified, the neighbor
set can be determined more explicitly. For example, when
is specified, the neighbor
set can be determined more explicitly. For example, when
 is an ordered set of sites and its elements index
the pixels of a 1D image, an interior site
is an ordered set of sites and its elements index
the pixels of a 1D image, an interior site 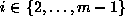 has
two nearest neighbors,
has
two nearest neighbors, 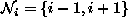 , and a site at the boundaries
(the two ends) has one neighbor each,
, and a site at the boundaries
(the two ends) has one neighbor each,
 and
and 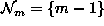 . When the sites in a regular
rectangular lattice
. When the sites in a regular
rectangular lattice 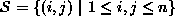 correspond to
the pixels of an
correspond to
the pixels of an 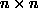 image in the 2D plane, an internal site
image in the 2D plane, an internal site
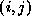 has four nearest neighbors as
has four nearest neighbors as
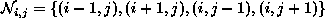 , a site at a boundary
has three and a site at the corners has two.
, a site at a boundary
has three and a site at the corners has two.
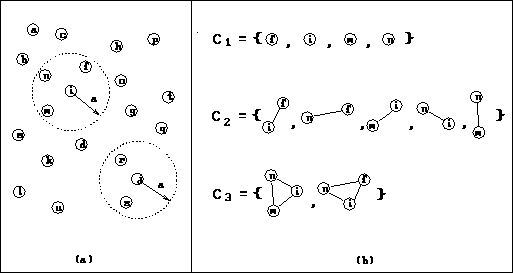
Figure 1.3: Neighborhood and cliques on a set of irregular sites.
For an irregular  , the neighbor set
, the neighbor set  of i is defined
in the same way as (1.13) to comprise
nearby sites within a radius of r
of i is defined
in the same way as (1.13) to comprise
nearby sites within a radius of r
The dist function needs to be defined appropriately for
non-point features. Alternatively, the neighborhood may be defined by
the Delaunay triangulation,(Algorithms for constructing a Delaunary triangulation in higher dimensional space can be found in [Bowyer 1981 ; Watson 1981]) or its dual, the
Voronoi polygons, of the sites [Besag 1975]. In general, the neighbor
sets
function needs to be defined appropriately for
non-point features. Alternatively, the neighborhood may be defined by
the Delaunay triangulation,(Algorithms for constructing a Delaunary triangulation in higher dimensional space can be found in [Bowyer 1981 ; Watson 1981]) or its dual, the
Voronoi polygons, of the sites [Besag 1975]. In general, the neighbor
sets 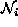 for an irregular
for an irregular 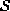 have varying shapes and sizes.
Irregular sites and their neighborhoods are illustrated in
Fig.1.3(a). The neighborhood areas for sites i and
j are marked by the dotted circles. The sizes of the two neighbor sets
are
have varying shapes and sizes.
Irregular sites and their neighborhoods are illustrated in
Fig.1.3(a). The neighborhood areas for sites i and
j are marked by the dotted circles. The sizes of the two neighbor sets
are  and
and 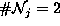 .
.
The pair 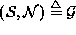 constitutes a graph in the usual sense
where
constitutes a graph in the usual sense
where 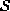 contains the nodes and
contains the nodes and 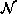 determines the links between
the notes according to the neighboring relationship. A clique
c for
determines the links between
the notes according to the neighboring relationship. A clique
c for  is defined as a subset of sites in
is defined as a subset of sites in
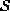 . It consists either of a single site
. It consists either of a single site  , or of a pair of
neighboring sites
, or of a pair of
neighboring sites 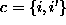 , or of a triple of neighboring sites
, or of a triple of neighboring sites
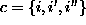 , and so on. The collections of single-site, pair-site
and triple-site cliques will be denoted by
, and so on. The collections of single-site, pair-site
and triple-site cliques will be denoted by 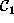 ,
, 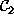 and
and 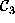 ,
respectively, where
,
respectively, where
and
Note that the sites in a clique are ordered, and 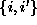 is
not the same clique as
is
not the same clique as  , and so on. The collection of all
cliques for
, and so on. The collection of all
cliques for 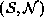 is
is
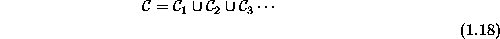
where "..." denotes possible sets of larger cliques.
The type of a clique for 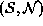 of a regular
lattice is determined by its size, shape and orientation.
Fig.1.2(d)-(h) show clique types for the first and
second order neighborhood systems for a lattice. The single-site and horizontal and vertical pair-site
cliques in (d) and (e) are all those for the first order neighborhood
system (a). The clique types for the second order neighborhood system
(b) include not only those in (d) and (e) but also diagonal pair-site
cliques (f) and triple-site (g) and quadruple-site (h) cliques. As the
order of the neighborhood system increases, the number of cliques grow
rapidly and so the involved computational expenses.
of a regular
lattice is determined by its size, shape and orientation.
Fig.1.2(d)-(h) show clique types for the first and
second order neighborhood systems for a lattice. The single-site and horizontal and vertical pair-site
cliques in (d) and (e) are all those for the first order neighborhood
system (a). The clique types for the second order neighborhood system
(b) include not only those in (d) and (e) but also diagonal pair-site
cliques (f) and triple-site (g) and quadruple-site (h) cliques. As the
order of the neighborhood system increases, the number of cliques grow
rapidly and so the involved computational expenses.
Cliques for irregular sites do not
have fixed shapes as those for a regular lattice. Therefore, their types
are essentially depicted by the number of involved sites. Consider the
four sites f, i, m and n within the circle in
Fig.1.3(a) in which m and n are supposed to be
neighbors to each other and so are n and f. Then the single-site,
pair-site and triple-site cliques associated with this set of sites are
shown in Fig.1.3(b).
The set 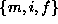 does not form a clique because f and m are not
neighbors.
does not form a clique because f and m are not
neighbors.