



Next: Gibbs Random Fields
Up: Markov Random Fields
Previous: Neighborhood System and Cliques
1.2.2
Let 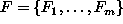 be a family of random variables defined
on the set
be a family of random variables defined
on the set 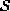 , in which each random variable
, in which each random variable 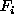 takes a value
takes a value
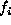 in
in 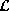 . The family F is called a random field.
We use the notation
. The family F is called a random field.
We use the notation  to denote the event
that
to denote the event
that 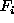 takes the value
takes the value 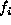 and the notation
and the notation 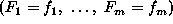 to denote the joint event. For simplicity, a joint event is
abbreviated as F=f where
to denote the joint event. For simplicity, a joint event is
abbreviated as F=f where 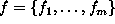 is a
configuration of F, corresponding to a
realization of the field. For a discrete label set
is a
configuration of F, corresponding to a
realization of the field. For a discrete label set 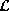 , the
probability that random variable
, the
probability that random variable 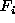 takes the value
takes the value 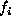 is denoted
is denoted
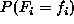 , abbreviated
, abbreviated  unless there is a need to elaborate
the expressions, and the joint probability is denoted
unless there is a need to elaborate
the expressions, and the joint probability is denoted
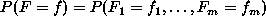 and abbreviated
and abbreviated 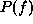 .
For a continuous
.
For a continuous 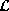 , we have probability
density functions
(p.d.f.'s),
, we have probability
density functions
(p.d.f.'s),
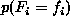 and
and  .
.
F is said to be a Markov random field on
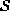 with respect to a neighborhood system
with respect to a neighborhood system 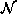 if and only if the
following two conditions are satisfied:
if and only if the
following two conditions are satisfied:


where 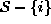 is the set difference,
is the set difference, 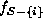 denotes the
set of labels at the sites in
denotes the
set of labels at the sites in 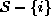 and
and
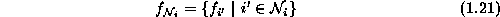
stands for the set of labels at the sites neighboring i. The
positivity is
assumed for some technical reasons and can usually be satisfied in
practice. For example, when the positivity condition is satisfied, the
joint probability 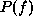 of any random field is uniquely determined by
its local conditional probabilities [Besag 1974]. The Markovianity
depicts
the local characteristics of F. A label interacts with only the neighboring labels. In other words, only neighboring
labels have direct interactions with each other. It is always possible to
select sufficiently large
of any random field is uniquely determined by
its local conditional probabilities [Besag 1974]. The Markovianity
depicts
the local characteristics of F. A label interacts with only the neighboring labels. In other words, only neighboring
labels have direct interactions with each other. It is always possible to
select sufficiently large  so that the Markovianity holds. The
largest neighborhood consists of all other sites. Any F is an MRF with
respect to such a neighborhood system.
so that the Markovianity holds. The
largest neighborhood consists of all other sites. Any F is an MRF with
respect to such a neighborhood system.
An MRF can have other properties such as homogeneity and isotropy.
It is said to be homogeneous if
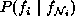 is regardless of the relative position of site
i in
is regardless of the relative position of site
i in  . The isotropy will
be illustrated in the next subsection with clique potentials.
. The isotropy will
be illustrated in the next subsection with clique potentials.
It may need to define for some problem a few coupled MRFs,
each defined on one of the spatially
interwoven sets of sites. For example, in the related tasks of image
restoration and edge detection, two MRFs, one for pixel values
(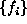 ) and the other for edge values (
) and the other for edge values (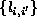 ), can be
defined on the image lattice and its dual lattice, respectively. They
are coupled to each other e.g.
via conditional probability
), can be
defined on the image lattice and its dual lattice, respectively. They
are coupled to each other e.g.
via conditional probability 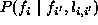 (see Section 2.3.1).
(see Section 2.3.1).
The concept of MRFs is a generalization of that of Markov processes
(MPs) which are widely used in sequence analysis.
An MP is defined on a domain of time rather than space. It is a sequence
(chain) of random variables 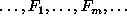 defined on
the time indices
defined on
the time indices 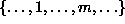 . An n-th order
unilateral MP satisfies
. An n-th order
unilateral MP satisfies
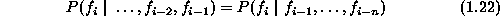
A bilateral or non-causal MP depends not only on the past but also on
the future. An n-th order bilateral MP satisfies
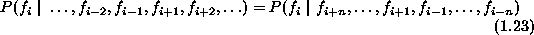
It is generalized into MRFs when the time indices are considered as
spatial indices.
There are two approaches for specifying an MRF, that in terms of the
conditional probabilities  and that in terms of
the joint probability
and that in terms of
the joint probability 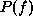 . Besag (1974) argues for the joint
probability approach in view of the disadvantages of the conditional
probability approach: Firstly, no obvious method is available for
deducing the joint probability from the associated conditional
probabilities. Secondly, the conditional probabilities themselves are
subject to some non-obvious and highly restrictive consistency
conditions. Thirdly, the natural specification of an equilibrium of
statistical process is in terms of the joint probability rather than the
conditional distribution of the variables. Fortunately, a theoretical
result about the equivalence between Markov random fields and Gibbs
distribution [Hammersley and Clifford 1971 ; Besag 1974] provides a
mathematically tractable means of specifying the joint probability of an
MRF.
. Besag (1974) argues for the joint
probability approach in view of the disadvantages of the conditional
probability approach: Firstly, no obvious method is available for
deducing the joint probability from the associated conditional
probabilities. Secondly, the conditional probabilities themselves are
subject to some non-obvious and highly restrictive consistency
conditions. Thirdly, the natural specification of an equilibrium of
statistical process is in terms of the joint probability rather than the
conditional distribution of the variables. Fortunately, a theoretical
result about the equivalence between Markov random fields and Gibbs
distribution [Hammersley and Clifford 1971 ; Besag 1974] provides a
mathematically tractable means of specifying the joint probability of an
MRF.




Next: Gibbs Random Fields
Up: Markov Random Fields
Previous: Neighborhood System and
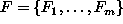 be a family of random variables defined
on the set
be a family of random variables defined
on the set 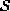 , in which each random variable
, in which each random variable 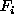 takes a value
takes a value
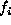 in
in 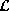 . The family F is called a random field.
We use the notation
. The family F is called a random field.
We use the notation  to denote the event
that
to denote the event
that 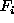 takes the value
takes the value 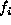 and the notation
and the notation 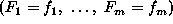 to denote the joint event. For simplicity, a joint event is
abbreviated as F=f where
to denote the joint event. For simplicity, a joint event is
abbreviated as F=f where 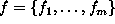 is a
configuration of F, corresponding to a
realization of the field. For a discrete label set
is a
configuration of F, corresponding to a
realization of the field. For a discrete label set 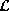 , the
probability that random variable
, the
probability that random variable 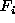 takes the value
takes the value 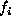 is denoted
is denoted
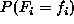 , abbreviated
, abbreviated  unless there is a need to elaborate
the expressions, and the joint probability is denoted
unless there is a need to elaborate
the expressions, and the joint probability is denoted
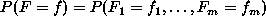 and abbreviated
and abbreviated 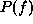 .
For a continuous
.
For a continuous 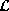 , we have probability
density functions
(p.d.f.'s),
, we have probability
density functions
(p.d.f.'s),
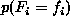 and
and  .
.
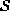 with respect to a neighborhood system
with respect to a neighborhood system 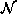 if and only if the
following two conditions are satisfied:
if and only if the
following two conditions are satisfied:


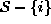 is the set difference,
is the set difference, 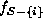 denotes the
set of labels at the sites in
denotes the
set of labels at the sites in 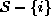 and
and
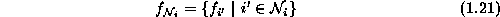
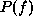 of any random field is uniquely determined by
its local conditional probabilities [
of any random field is uniquely determined by
its local conditional probabilities [ so that the Markovianity holds. The
largest neighborhood consists of all other sites. Any F is an MRF with
respect to such a neighborhood system.
so that the Markovianity holds. The
largest neighborhood consists of all other sites. Any F is an MRF with
respect to such a neighborhood system.
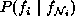 is regardless of the relative position of site
i in
is regardless of the relative position of site
i in  .
. 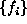 ) and the other for edge values (
) and the other for edge values (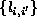 ), can be
defined on the image lattice and its dual lattice, respectively. They
are coupled to each other e.g.
via conditional probability
), can be
defined on the image lattice and its dual lattice, respectively. They
are coupled to each other e.g.
via conditional probability 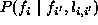 (see Section
(see Section 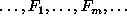 defined on
the time indices
defined on
the time indices 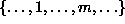 . An n-th order
unilateral MP satisfies
. An n-th order
unilateral MP satisfies
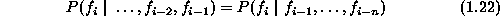
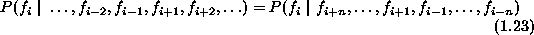
 and that in terms of
the joint probability
and that in terms of
the joint probability 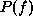 . Besag (1974) argues for the joint
probability approach in view of the disadvantages of the conditional
probability approach: Firstly, no obvious method is available for
deducing the joint probability from the associated conditional
probabilities. Secondly, the conditional probabilities themselves are
subject to some non-obvious and highly restrictive consistency
conditions. Thirdly, the natural specification of an equilibrium of
statistical process is in terms of the joint probability rather than the
conditional distribution of the variables. Fortunately, a theoretical
result about the equivalence between Markov random fields and Gibbs
distribution [
. Besag (1974) argues for the joint
probability approach in view of the disadvantages of the conditional
probability approach: Firstly, no obvious method is available for
deducing the joint probability from the associated conditional
probabilities. Secondly, the conditional probabilities themselves are
subject to some non-obvious and highly restrictive consistency
conditions. Thirdly, the natural specification of an equilibrium of
statistical process is in terms of the joint probability rather than the
conditional distribution of the variables. Fortunately, a theoretical
result about the equivalence between Markov random fields and Gibbs
distribution [