



Next: Useful MRF Models
Up: Markov Random Fields
Previous: Markov-Gibbs Equivalence
1.2.5
It is known that the choices of clique potential functions for a
specific MRF is not unique; there may exist many equivalent choices
which specify the same Gibbs distribution. However, there exists a
unique normalized potential, called the canonical potential, for
every MRF [Griffeath 1976].
Let 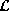 be a countable label set. A clique potential function
be a countable label set. A clique potential function 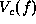 is said to be normalized if
is said to be normalized if
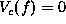 whenever for some
whenever for some  ,
, 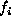 takes a particular value in
takes a particular value in
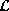 . The particular value can be any element in
. The particular value can be any element in 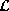 , e.g.
0 in
, e.g.
0 in
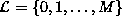 . Griffeath (1976)
establishes the mathematical relationship between an MRF distribution
. Griffeath (1976)
establishes the mathematical relationship between an MRF distribution
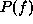 and the unique canonical representation of clique potentials
and the unique canonical representation of clique potentials
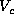 in the corresponding Gibbs distribution [Griffeath 1976 ; Kindermann and Snell 1980]. The result is described
below.
in the corresponding Gibbs distribution [Griffeath 1976 ; Kindermann and Snell 1980]. The result is described
below.
Let F be a random field on a finite set 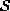 with local
characteristics
with local
characteristics 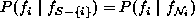 .
Then F is a Gibbs field with canonical potential function
defined by the following:
.
Then F is a Gibbs field with canonical potential function
defined by the following:
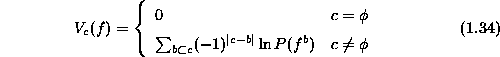
where  denotes the empty set, |c-b| is the number of elements
in the set c-b and
denotes the empty set, |c-b| is the number of elements
in the set c-b and

is the configuration which agrees with f on set b but assigns the
value 0 to all sites outside of b. For nonempty c, the potential
can also be obtained as
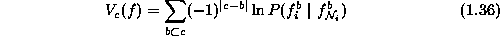
where i is any element in b. Such canonical potential function is
unique for the corresponding MRF. Using this result, the canonical
 can be computed if
can be computed if 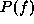 is known.
is known.
However, in MRF modeling using Gibbs distributions, 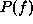 is defined
after
is defined
after 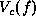 is determined and therefore, it is difficult to compute
the canonical
is determined and therefore, it is difficult to compute
the canonical 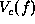 from
from 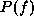 directly. Nonetheless, there is an
indirect way: Use a non-canonical representation to derive
directly. Nonetheless, there is an
indirect way: Use a non-canonical representation to derive 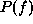 and
then canonicalize it using Griffeath's result to obtain the unique
canonical representation.
and
then canonicalize it using Griffeath's result to obtain the unique
canonical representation.
The normalized potential functions appear to be immediately useful. For
instance, for the sake of economy, one would use the minimal number of
clique potentials or parameters to represent an MRF for a given
neighborhood system. The concept of normalized potential functions can
be used to reduce the number of nonzero clique parameters (see
Chapter 6).
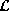 be a countable label set. A clique potential function
be a countable label set. A clique potential function 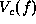 is said to be normalized if
is said to be normalized if
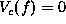 whenever for some
whenever for some  ,
, 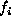 takes a particular value in
takes a particular value in
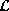 . The particular value can be any element in
. The particular value can be any element in 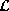 , e.g.
0 in
, e.g.
0 in
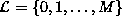 . Griffeath (1976)
establishes the mathematical relationship between an MRF distribution
. Griffeath (1976)
establishes the mathematical relationship between an MRF distribution
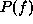 and the unique canonical representation of clique potentials
and the unique canonical representation of clique potentials
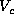 in the corresponding Gibbs distribution [Griffeath 1976 ; Kindermann and Snell 1980]. The result is described
below.
in the corresponding Gibbs distribution [Griffeath 1976 ; Kindermann and Snell 1980]. The result is described
below.
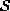 with local
characteristics
with local
characteristics 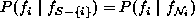 .
Then F is a Gibbs field with canonical potential function
defined by the following:
.
Then F is a Gibbs field with canonical potential function
defined by the following:
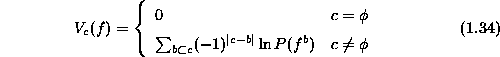
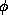 denotes the empty set, |c-b| is the number of elements
in the set c-b and
denotes the empty set, |c-b| is the number of elements
in the set c-b and

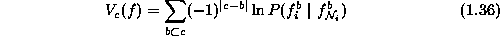
 can be computed if
can be computed if 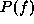 is known.
is known.
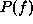 is defined
after
is defined
after 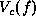 is determined and therefore, it is difficult to compute
the canonical
is determined and therefore, it is difficult to compute
the canonical 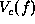 from
from 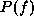 directly. Nonetheless, there is an
indirect way: Use a non-canonical representation to derive
directly. Nonetheless, there is an
indirect way: Use a non-canonical representation to derive 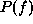 and
then canonicalize it using Griffeath's result to obtain the unique
canonical representation.
and
then canonicalize it using Griffeath's result to obtain the unique
canonical representation.