



Next: Optimization-Based Vision
Up: Useful MRF Models
Previous: The Smoothness Prior
1.3.4
A hierarchical two-level Gibbs model has been proposed to
represent both noise-contaminated and textured images
[Derin and Cole 1986; Derin and Elliott 1987]. The higher level Gibbs distribution uses an
isotropic random field, e.g.
MLL, to characterize the blob-like region
formation process. A lower level Gibbs distribution describes the
filling-in in each region. The filling-in may be independent noise or a
type of texture, both of which can be characterized by Gibbs
distributions. This provides a convenient approach for MAP-MRF modeling.
In segmentation of noisy and textured image
[Derin and Cole 1986; Derin and Elliott 1987; Lakshmanan and Derin 1989; Hu and Fahmy 1987; Won and Derin 1992], for example, the
higher level determines the prior of f for the region process while
the lower level Gibbs contributes to the conditional probability of the
data given f. Note that different levels of MRFs in the hierarchy can
have different neighborhood systems.
Various hierarchical Gibbs models result according to what are chosen
for the regions and for the filling-in's, respectively. For example,
each region may be filled in by an auto-normal texture
[Simchony and Chellappa 1988; Won and Derin 1992] or an auto-binomial
texture [Hu and Fahmy 1987]; the MLL for the region
formation may be substituted by another appropriate MRF. The
hierarchical MRF model for textured regions will be further discussed in
Section 2.4.1.
A drawback of the hierarchical model is that the conditional probability
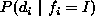 for regions given by
for regions given by 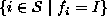 can
not always be written exactly. For example, when the lower level MRF is
a texture modeled as an auto-normal field, its joint distribution over an
irregularly shaped region is not known. This difficulty may be overcome
by using approximate schemes such as pseudo-likelihood to be
introduced in Section 6.1 or by using
the eigen-analysis method [Wu and Leahy 1993].
can
not always be written exactly. For example, when the lower level MRF is
a texture modeled as an auto-normal field, its joint distribution over an
irregularly shaped region is not known. This difficulty may be overcome
by using approximate schemes such as pseudo-likelihood to be
introduced in Section 6.1 or by using
the eigen-analysis method [Wu and Leahy 1993].
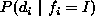 for regions given by
for regions given by 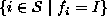 can
not always be written exactly. For example, when the lower level MRF is
a texture modeled as an auto-normal field, its joint distribution over an
irregularly shaped region is not known. This difficulty may be overcome
by using approximate schemes such as pseudo-likelihood to be
introduced in Section 6.1 or by using
the eigen-analysis method [Wu and Leahy 1993].
can
not always be written exactly. For example, when the lower level MRF is
a texture modeled as an auto-normal field, its joint distribution over an
irregularly shaped region is not known. This difficulty may be overcome
by using approximate schemes such as pseudo-likelihood to be
introduced in Section 6.1 or by using
the eigen-analysis method [Wu and Leahy 1993].