



Next: Regularization
Up: Bayes Labeling of MRFs
Previous: Bayes Estimation
1.5.2
In the MAP-MRF labeling, 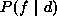 is the posterior distribution of
an MRF. An important step in Bayes labeling of MRFs is to derive this
distribution. Here we use a simple formulation of MRF restoration as an
example to illustrate MAP-MRF labeling. Assuming the underlying surface is
flat, then the joint prior distribution is
is the posterior distribution of
an MRF. An important step in Bayes labeling of MRFs is to derive this
distribution. Here we use a simple formulation of MRF restoration as an
example to illustrate MAP-MRF labeling. Assuming the underlying surface is
flat, then the joint prior distribution is
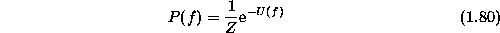
where 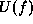 is the prior energy given in
(1.57). Assuming that the observation is the
truth plus the independent Gaussian noise,
is the prior energy given in
(1.57). Assuming that the observation is the
truth plus the independent Gaussian noise,  , where
, where 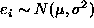 , then the likelihood density is
, then the likelihood density is
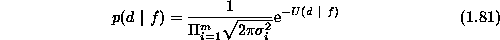
where
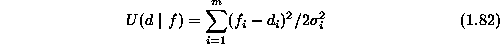
is the likelihood energy. Now the posterior probability is
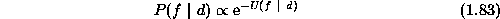
where
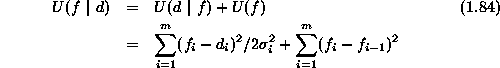
is the posterior energy. The MAP estimate is equivalently found
by minimizing the posterior energy

When the parameters  are given so that
are given so that 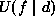 is
fully specified, the MAP-MRF labeling solution is completely
defined.
is
fully specified, the MAP-MRF labeling solution is completely
defined.
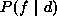 is the posterior distribution of
an MRF. An important step in Bayes labeling of MRFs is to derive this
distribution. Here we use a simple formulation of MRF restoration as an
example to illustrate MAP-MRF labeling. Assuming the underlying surface is
flat, then the joint prior distribution is
is the posterior distribution of
an MRF. An important step in Bayes labeling of MRFs is to derive this
distribution. Here we use a simple formulation of MRF restoration as an
example to illustrate MAP-MRF labeling. Assuming the underlying surface is
flat, then the joint prior distribution is
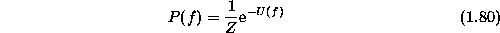
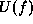 is the prior energy given in
(
is the prior energy given in
( , where
, where 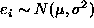 , then the likelihood density is
, then the likelihood density is
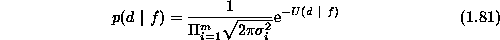
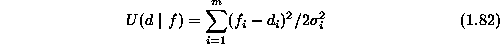
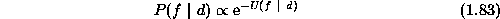
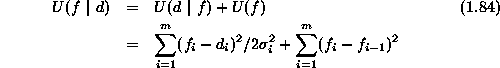

 are given so that
are given so that 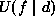 is
fully specified, the MAP-MRF labeling solution is completely
defined.
is
fully specified, the MAP-MRF labeling solution is completely
defined.