



Next: Summary of MAP-MRF Approach
Up: Bayes Labeling of MRFs
Previous: MAP-MRF Labeling
1.5.3
The MAP labeling with a prior potential of the form 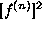 introduced in Section 1.3.3 is equivalent to the
regularization of an ill-posed problem. A problem is mathematically an
ill-posed problem [Tikhonov and Arsenin 1977] in
the Hadamard sense if its solution (1) does not exist, (2) is not
unique or (3) does not depend continuously on the initial data. An
example is surface reconstruction or interpolation. A problem therein is
that there are infinitely many ways to determine the interpolated
surface values if only the constraint from the data is used. Additional
constraints are needed to guarantee the uniqueness of the solution to
make the problem well-posed. An important such constraint is
smoothness. By imposing the smoothness constraint, the analytic
regularization method converts an ill-posed problem into a well-posed
one. This has been used in solving low level problems such as surface
reconstruction from stereo [Grimson 1981], optical flow
[Horn and Schunck 1981], shape-from-shading [Ikeuchi and Horn 1981], and motion
analysis [Hildreth 1984]. A review of earlier work of
regularization in vision is given by [Poggio et al. 1985].
Relationships between regularization and smoothing splines for vision
processing are investigated by [Terzopoulos 1986b ; Lee and Pavlidis 1987].
introduced in Section 1.3.3 is equivalent to the
regularization of an ill-posed problem. A problem is mathematically an
ill-posed problem [Tikhonov and Arsenin 1977] in
the Hadamard sense if its solution (1) does not exist, (2) is not
unique or (3) does not depend continuously on the initial data. An
example is surface reconstruction or interpolation. A problem therein is
that there are infinitely many ways to determine the interpolated
surface values if only the constraint from the data is used. Additional
constraints are needed to guarantee the uniqueness of the solution to
make the problem well-posed. An important such constraint is
smoothness. By imposing the smoothness constraint, the analytic
regularization method converts an ill-posed problem into a well-posed
one. This has been used in solving low level problems such as surface
reconstruction from stereo [Grimson 1981], optical flow
[Horn and Schunck 1981], shape-from-shading [Ikeuchi and Horn 1981], and motion
analysis [Hildreth 1984]. A review of earlier work of
regularization in vision is given by [Poggio et al. 1985].
Relationships between regularization and smoothing splines for vision
processing are investigated by [Terzopoulos 1986b ; Lee and Pavlidis 1987].
A regularization solution is obtained by minimizing an energy of
the following form
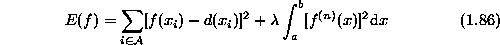
where  is a set of indices to the sample data points,
is a set of indices to the sample data points, 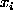 's are
the locations of the data points,
's are
the locations of the data points,  is a weighting factor
and
is a weighting factor
and 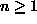 is an integer number. The first term on the RHS, called the
closeness term, imposes the constraint from the
data d. The second term, called the smoothness term or the
regularizer, imposes the a priori smoothness constraint on the solution.
It is desired to minimize both but they may not be each minimized
simultaneously. The two constraints are balanced by
is an integer number. The first term on the RHS, called the
closeness term, imposes the constraint from the
data d. The second term, called the smoothness term or the
regularizer, imposes the a priori smoothness constraint on the solution.
It is desired to minimize both but they may not be each minimized
simultaneously. The two constraints are balanced by  . Any f
minimizing (1.86) is a smooth solution in the
so-called Sobolev space
. Any f
minimizing (1.86) is a smooth solution in the
so-called Sobolev space 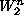 (In the Sobolev space, every point f is a function whose n-1 derivative
(In the Sobolev space, every point f is a function whose n-1 derivative  is absolutely continuous and whose n-th derivative
is absolutely continuous and whose n-th derivative 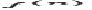 is square integrable) .
Different types of regularizers impose different types of smoothness
constraints. Section 1.3.3 has described smoothness
priors for some classes of surfaces. A study of the quadratic smoothness
constraints is given in [Snyder 1991].
is square integrable) .
Different types of regularizers impose different types of smoothness
constraints. Section 1.3.3 has described smoothness
priors for some classes of surfaces. A study of the quadratic smoothness
constraints is given in [Snyder 1991].
Under certain conditions, the MAP labeling of MRFs is equivalent to a
regularization solution [Marroquin et al. 1987]. These conditions are (1)
that the likelihood energy is due to additive white Gaussian noise and
(2) that the prior assumption is the smoothness. Letting n=1 and
discretizing x, (1.86) becomes the
posterior energy (1.84) for the restoration of flat
surfaces (in 1D). When the regularizer takes the form of the rod
(1.61), it encodes the smoothness of planar surfaces (in 1D).
The 2D counterparts are the membrane (1.60),
(1.65) and the plate (1.66).
MRFs is more general than regularization in that it can encode not only
the smoothness prior but also priors of other constraints. MRF-based
models have to be chosen among the two when the priors are due to those
other than the smoothness, e.g.
in texture modeling and analysis.
However, regularization can deal with spatially continuous fields
whereas MRFs, which in this book are spatially discrete, cannot. When
the problem under consideration involves concepts such as
discontinuities, the analytical regularization is more suitable for the
analysis. This is why we will study the issue of discontinuities, in
Chapter 3, from regularization viewpoint.




Next: Summary of MAP-MRF Approach
Up: Bayes Labeling of MRFs
Previous: MAP-MRF Labeling
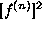 introduced in Section 1.3.3 is equivalent to the
regularization of an ill-posed problem. A problem is mathematically an
ill-posed problem [Tikhonov and Arsenin 1977] in
the Hadamard sense if its solution (1) does not exist, (2) is not
unique or (3) does not depend continuously on the initial data. An
example is surface reconstruction or interpolation. A problem therein is
that there are infinitely many ways to determine the interpolated
surface values if only the constraint from the data is used. Additional
constraints are needed to guarantee the uniqueness of the solution to
make the problem well-posed. An important such constraint is
smoothness. By imposing the smoothness constraint, the analytic
regularization method converts an ill-posed problem into a well-posed
one. This has been used in solving low level problems such as surface
reconstruction from stereo [Grimson 1981], optical flow
[Horn and Schunck 1981], shape-from-shading [Ikeuchi and Horn 1981], and motion
analysis [Hildreth 1984]. A review of earlier work of
regularization in vision is given by [Poggio et al. 1985].
Relationships between regularization and smoothing splines for vision
processing are investigated by [Terzopoulos 1986b ; Lee and Pavlidis 1987].
introduced in Section 1.3.3 is equivalent to the
regularization of an ill-posed problem. A problem is mathematically an
ill-posed problem [Tikhonov and Arsenin 1977] in
the Hadamard sense if its solution (1) does not exist, (2) is not
unique or (3) does not depend continuously on the initial data. An
example is surface reconstruction or interpolation. A problem therein is
that there are infinitely many ways to determine the interpolated
surface values if only the constraint from the data is used. Additional
constraints are needed to guarantee the uniqueness of the solution to
make the problem well-posed. An important such constraint is
smoothness. By imposing the smoothness constraint, the analytic
regularization method converts an ill-posed problem into a well-posed
one. This has been used in solving low level problems such as surface
reconstruction from stereo [Grimson 1981], optical flow
[Horn and Schunck 1981], shape-from-shading [Ikeuchi and Horn 1981], and motion
analysis [Hildreth 1984]. A review of earlier work of
regularization in vision is given by [Poggio et al. 1985].
Relationships between regularization and smoothing splines for vision
processing are investigated by [Terzopoulos 1986b ; Lee and Pavlidis 1987].
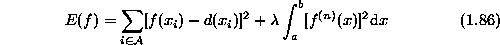
 is a set of indices to the sample data points,
is a set of indices to the sample data points, 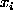 's are
the locations of the data points,
's are
the locations of the data points,  is a weighting factor
and
is a weighting factor
and 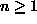 is an integer number. The first term on the RHS, called the
closeness term,
is an integer number. The first term on the RHS, called the
closeness term,  . Any f
minimizing (
. Any f
minimizing (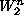 (In the Sobolev space, every point f is a function whose n-1 derivative
(In the Sobolev space, every point f is a function whose n-1 derivative  is absolutely continuous and whose n-th derivative
is absolutely continuous and whose n-th derivative 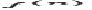 is square integrable) .
Different types of regularizers impose different types of smoothness
constraints. Section
is square integrable) .
Different types of regularizers impose different types of smoothness
constraints. Section