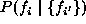 , where
, where
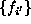 denotes the set of labels at the other sites
denotes the set of labels at the other sites 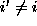 , or
globally as the joint probability
, or
globally as the joint probability 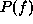 . Because local information is
more directly observed, it is normal that a global inference is made
based on local properties.
. Because local information is
more directly observed, it is normal that a global inference is made
based on local properties.
1.1.4
The use of contextual information is ultimately indispensable in image understanding [Pavlidis 1986]. The use of contextual information in image analysis and pattern recognition dates back to [Chow 1962 ; Abend et al. 1965]. In [Chow 1962] character recognition is considered as a statistical decision problem. A nearest neighborhood dependence of pixels on an image lattice is obtained by going beyond the assumption of statistical independence. Information on the nearest neighborhood is used to calculate conditional probabilities. That system also includes parameter estimation from sample characters; recognition is done by using the estimated parameters. The work by [Abend et al. 1965] is probably the earliest work using the Markov assumption for pattern recognition. There, a Markov mesh model is used to reduce the number of parameters required for the processing using contextual constraints. Fu and Yu (1980) use MRFs defined on an image lattice to develop a class of pattern classifiers for remote sensing image classification. Another development of context-based models is relaxation labeling (RL) [Rosenfeld et al. 1976]. RL is a class of iterative procedures which use contextual constraints to reduce ambiguities in image analysis. A theory is given in [Haralick 1983] to explain RL from a Bayes point of view.
In probability terms, contextual constraints may be expressed locally in
terms of conditional probabilities 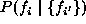 , where
, where
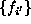 denotes the set of labels at the other sites
denotes the set of labels at the other sites 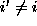 , or
globally as the joint probability
, or
globally as the joint probability 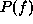 . Because local information is
more directly observed, it is normal that a global inference is made
based on local properties.
. Because local information is
more directly observed, it is normal that a global inference is made
based on local properties.
In situations where labels are independent one another (no context), the joint probability is the product of the local ones
The above implies conditional independence
Therefore, a global labeling f can be computed by considering each
label 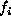 locally. This is advantageous for problem solving.
locally. This is advantageous for problem solving.
In the presence of context, labels are mutually dependent. The simple relationships expressed in (1.10) and (1.11) do not hold any more. How to make a global inference using local information becomes a non-trivial task. Markov random field theory provides a mathematical foundation for solving this problem.