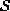 with respect to
with respect to 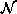 if
and only if F is a GRF on
if
and only if F is a GRF on  with respect to
with respect to 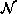 . Many proofs of the theorem
exist, e.g.
in [Besag 1974 ; Moussouris 1974 ; Kindermann and Snell 1980].
. Many proofs of the theorem
exist, e.g.
in [Besag 1974 ; Moussouris 1974 ; Kindermann and Snell 1980].
1.2.4
An MRF is characterized by its local property (the Markovianity)
whereas a GRF is characterized by its global property (the Gibbs
distribution). The Hammersley-Clifford theorem
[Hammersley and Clifford 1971]
establishes the equivalence of these two types of properties. The
theorem states that F is an MRF on 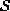 with respect to
with respect to 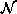 if
and only if F is a GRF on
if
and only if F is a GRF on  with respect to
with respect to 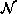 . Many proofs of the theorem
exist, e.g.
in [Besag 1974 ; Moussouris 1974 ; Kindermann and Snell 1980].
. Many proofs of the theorem
exist, e.g.
in [Besag 1974 ; Moussouris 1974 ; Kindermann and Snell 1980].
A proof that a GRF is an MRF is given as follows. Let 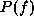 be a Gibbs
distribution on
be a Gibbs
distribution on 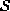 with respect to the neighborhood system
with respect to the neighborhood system 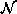 .
Consider the conditional probability
.
Consider the conditional probability
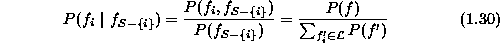
where 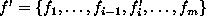 is any configuration
which agrees with f at all sites except possibly i. Writing
is any configuration
which agrees with f at all sites except possibly i. Writing
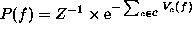 out
gives (This also provides a formula for calculating the conditional probability
out
gives (This also provides a formula for calculating the conditional probability 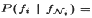
 from potential functions.)
from potential functions.)
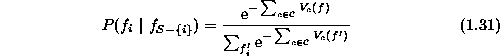
Divide  into two set
into two set 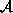 and
and 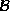 with
with 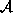 consisting of
cliques containing i and
consisting of
cliques containing i and 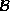 cliques not containing i. Then
the above can be written as
cliques not containing i. Then
the above can be written as
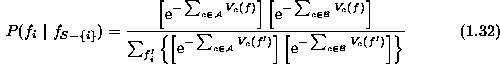
Because 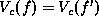 for any clique c that does not contain i,
for any clique c that does not contain i,
 cancels from both the numerator and
denominator. Therefore, this probability depends only on the potentials
of the cliques containing i,
cancels from both the numerator and
denominator. Therefore, this probability depends only on the potentials
of the cliques containing i,

that is, it depends on labels at i's neighbors. This proves that a Gibbs random field is a Markov random field. The proof that an MRF is a GRF is much more involved; a result to be described in the next subsection, which is about the unique GRF representation [Griffeath 1976], provides such a proof.
The practical value of the theorem is that it provides a simple way of
specifying the joint probability. One can specify the joint probability
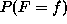 by specifying the clique potential functions
by specifying the clique potential functions 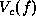 and
chooses appropriate potential functions for desired system behavior. In
this way, he encodes the a priori knowledge or preference about
interactions between labels.
and
chooses appropriate potential functions for desired system behavior. In
this way, he encodes the a priori knowledge or preference about
interactions between labels.
How to choose the forms and parameters of the potential functions for a proper encoding of constraints is a major topic in MRF modeling. The forms of the potential functions determine the form of the Gibbs distribution. When all the parameters involved in the potential functions are specified, the Gibbs distribution is completely defined. Defining the functional forms is the theme in Chapters 2 -- 5 while estimating parameters is the subject in Chapters 6 and 7.
To calculate the joint probability of an MRF, which is a Gibbs
distribution, it is necessary to evaluate the partition function
( 1.25). Because it is the sum over a
combinatorial number of configurations in 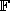 , the computation is
usually intractable. The explicit evaluation can be avoided in
maximum-probability based MRF vision models when
, the computation is
usually intractable. The explicit evaluation can be avoided in
maximum-probability based MRF vision models when 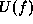 contains no
unknown parameters, as we will see subsequently. However, this is not
true when the parameter estimation is also a part of the problem. In the
latter case, the energy function
contains no
unknown parameters, as we will see subsequently. However, this is not
true when the parameter estimation is also a part of the problem. In the
latter case, the energy function 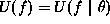 is also a
function of parameters
is also a
function of parameters 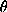 and so is the partition function
and so is the partition function
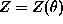 . The evaluation of
. The evaluation of  is required. To circumvent
the formidable difficulty therein, the joint probability is often
approximated in practice. Several approximate formulae will be
introduced in Chapter 6 where the problem of MRF
parameter estimation is the subject.
is required. To circumvent
the formidable difficulty therein, the joint probability is often
approximated in practice. Several approximate formulae will be
introduced in Chapter 6 where the problem of MRF
parameter estimation is the subject.