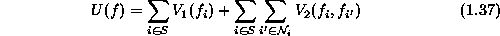
1.3.1
Contextual constraints on two labels are the lowest order constraints to convey contextual information. They are widely used because of their simple form and low computational cost. They are encoded in the Gibbs energy as pair-site clique potentials. With clique potentials of up to two sites, the energy takes the form
where ``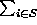
'' is equivalent to ``
''
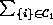and ``
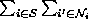'' to
``
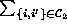''. The above is a special case of
(1.27), which we call a second-order energy
because it involves up to pair-site cliques. It
is most frequently used form owing to the mentioned feature that it is
the simplest in form but conveys contextual information. A specific GRF
or MRF can be specified by proper selection of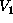 
's and 
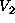's. Some
important such GRF models are described subsequently. Derin and Kelly
(1989) present a systematic study and categorization
of Markov random processes and fields in terms of what they call
strict-sense Markov and wide-sense Markov properties.
When 
and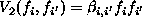 
, where
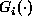are arbitrary functions and 
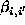are constants
reflecting the pair-site interaction between i and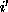 
, the energy is
The above is called auto-models [Besag 1974]. The auto-models
can be further classified according to assumptions made about individual
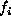's.
An auto-model is said to be an auto-logistic model,
if the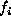 
's take on values in the discrete
label set 
(or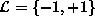 
). The corresponding energy
is of the following form
where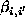 
can be viewed as the interaction
coefficients. When 
is the
nearest neighborhood system on a lattice (4 nearest neighbors on a 2D
lattice or 2 nearest neighbors on a 1D lattice), the auto-logistic model
is reduced to the Ising model. The conditional
probability for the auto-logistic model with 
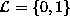is
When the distribution is homogeneous, we have
and 
regardless of i and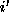 
.
An auto-model is said to be an auto-binomial model
if the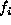 
's take on values in
and every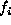 
has a conditionally binomial
distribution of M trials and probability of success q
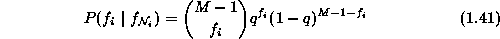
where
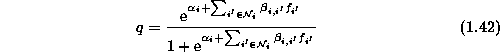
The corresponding energy takes the following form
It reduces to the auto-logistic model when M=1.
An auto-model is said to be an auto-normal model
, also called a Gaussian MRF [Chellappa 1985]
, if the label set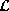 
is
the real line and the joint distribution is multivariate normal. Its
conditional p.d.f. is
It is the normal distribution with conditional mean
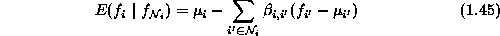
and conditional variance
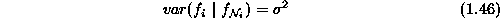
The joint probability is a Gibbs distribution
where f is viewed as a vector,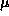 
is the 
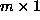vector of the
conditional means, and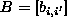 
is the 
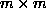interaction matrix whose
elements are unity and off-diagonal element at (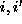
) is
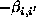, i.e.
with
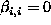. Therefore, the single-site and pair-site clique
potential functions for the auto-normal model are
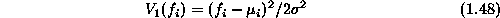
and
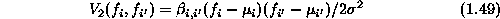
respectively. A field of independent Gaussian noise is a special MRF
whose Gibbs energy consists of only single-site clique potentials.
Because all higher order clique potentials are zero, there is no
contextual interaction in the independent Gaussian noise. B is related
to the covariance matrix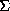 
by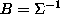 
. The necessary and
sufficient condition for (1.47) to be a valid p.d.f.
is that B is symmetric and positive definite.
A related but different model is the simultaneous auto-regression (SAR) model. Unlike the auto-normal model which is defined by the m conditional p.d.f.'s, this model is defined by a set of m equations
where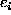 
are independent Gaussian, 
.
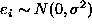It also generates the class of all multivariate
normal distributions but with joint p.d.f. as
where B is defined as before. Any SAR model is an auto-normal model
with the B matrix in (1.47) being
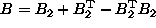where 
. The
reverse can also be done, though in a rather unnatural way via Cholesky
decomposition [Ripley 1981]. Therefore, both models can have their
p.d.f.'s in the form (1.47). However, for
(1.51) to be a valid p.d.f., it requires only
that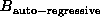 
be non-singular.
