



Next: Optimality Criteria
Up: Optimization-Based Vision
Previous: Role of Energy Functions
1.4.3
In pattern recognition, there are two basic approaches to formulating an
energy function: parametric and nonparametric. In the parametric
approach, the types of underlying distributions are known and the
distributions are parameterized by a few parameters. Therefore, the
functional form of the energy can be obtained and the energy function is
completely defined when the parameters are specified.
In the nonparametric approach, sometimes called distribution free
approach, no assumptions about the distributions are made. There, a
distribution is either estimated from the data or approximated by a
pre-specified basis functions with several unknown parameters in it to
be estimated. In the latter case, the pre-specified basis functions will
determine the functional form of the energy.
Despite the terms parametric and nonparametric, both approaches are
somewhat parametric in nature. This is because in any case, there are
always parameters that must be determined to define the energy function.
The two most important aspects of an energy function are its form and
the involved parameters. The form and parameters together define the
energy function which in turn defines the minimal solution. The form
depends on assumptions about the solution f and the observed data d.
We express this using the notation 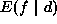 . Denote the set of
involved parameters by
. Denote the set of
involved parameters by 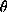 . With
. With 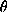 , the energy is expressed
further as
, the energy is expressed
further as 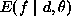 . In general, given the functional form
for E, a different d or
. In general, given the functional form
for E, a different d or 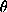 defines a different energy
function,
defines a different energy
function, 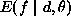 , w.r.t. f and hence a (possibly)
different minimal solution
, w.r.t. f and hence a (possibly)
different minimal solution 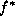 .
.
Since the parameters are part of the definition of the energy function
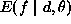 , the minimal solution
, the minimal solution 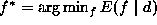 is not completely defined if the parameters are not specified even
if the functional form is known. These parameters must be specified or
estimated by some means. This is an important area of study in the MRF
vision modeling.
is not completely defined if the parameters are not specified even
if the functional form is known. These parameters must be specified or
estimated by some means. This is an important area of study in the MRF
vision modeling.
Having formulated an energy function, one would ask the following
question: Is the formulation correct? In other words, whether the
minimal solution 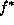 corresponds to the correct one? Before answering
this, let us make some remarks on the question. First, ``the minimal
solution''
corresponds to the correct one? Before answering
this, let us make some remarks on the question. First, ``the minimal
solution'' 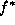 is meant to be the global one, or a global one if there
are multiple global minima. Second, ``the correct solution'', denoted
is meant to be the global one, or a global one if there
are multiple global minima. Second, ``the correct solution'', denoted
 , is said here in the subjective sense of our own
perception. For example, in edge detection, we run a program and get an
edge map as a solution; but we find that some edges are missing and some
false edges appear. This is the case where the solution differs from the
subjectively correct solution of ours.
, is said here in the subjective sense of our own
perception. For example, in edge detection, we run a program and get an
edge map as a solution; but we find that some edges are missing and some
false edges appear. This is the case where the solution differs from the
subjectively correct solution of ours.
In the ideal case, the global minimal solution 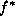 should
correspond to the correct solution
should
correspond to the correct solution 

A formulation is correct for d if the above holds. This
reflects our desire to encode our ability into the machine and is the
most important principle in formulating an energy function. For the time
being, we do not expect the machine to surpass our ability and therefore
we desire that the minimum of an energy function, or the machine's
solution, be consistent with ours. Whenever there is a difference, we
assume that our perception is correct and the difference is due to
problems in the programs we wrote into the machine, such as incorrect
assumptions made in the modeling stage.

Figure 1.5: Two global minima a and b and a local minimum c.
Let there be N sets of observations 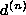 (
(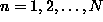 ).
Supposing that
).
Supposing that 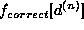 is the correct solution for
is the correct solution for
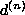 in our perception, we say that the functional form of the
energy E and the chosen parameters
in our perception, we say that the functional form of the
energy E and the chosen parameters 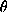 are correct for the N
observations if the following
are correct for the N
observations if the following
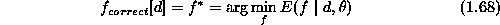
where 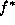 is the energy minimum, holds for each
is the energy minimum, holds for each 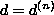 . Let
. Let
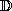 be the space of all possible observations. If
Eq.(1.68) holds for all
be the space of all possible observations. If
Eq.(1.68) holds for all 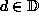 , we say that
E and
, we say that
E and  , hence the formulation, is entirely correct.
, hence the formulation, is entirely correct.
A formulation may not be absolutely correct. For example, a formulation
for edge detection may give solutions having some missing or falsely
detected edges or having some inaccurate edge locations. The quality of
a formulation may be measured by some distance between the global energy
minimum 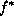 and the correct solution
and the correct solution  . Ideally, it should
be zero.
. Ideally, it should
be zero.
What about multiple global minima? Suppose there are two global minima
for which 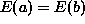 , as in Fig.1.5. Both solutions
a and b should be equally good if the formulation is correct. If one
of them is better than the other in our perception, then there is still
room to improve the formulation of
, as in Fig.1.5. Both solutions
a and b should be equally good if the formulation is correct. If one
of them is better than the other in our perception, then there is still
room to improve the formulation of 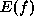 . The improvement is made by
adjusting either the functional form or the parameters so that the
improved energy function embeds the better solution as its unique
global minimum.
. The improvement is made by
adjusting either the functional form or the parameters so that the
improved energy function embeds the better solution as its unique
global minimum.



 Optimality Criteria
Up: Optimization-Based Vision
Previous: Role of Energy Functions
Optimality Criteria
Up: Optimization-Based Vision
Previous: Role of Energy Functions
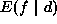 . Denote the set of
involved parameters by
. Denote the set of
involved parameters by 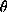 . With
. With 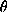 , the energy is expressed
further as
, the energy is expressed
further as 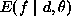 . In general, given the functional form
for E, a different d or
. In general, given the functional form
for E, a different d or 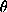 defines a different energy
function,
defines a different energy
function, 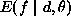 , w.r.t. f and hence a (possibly)
different minimal solution
, w.r.t. f and hence a (possibly)
different minimal solution 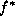 .
.
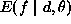 , the minimal solution
, the minimal solution 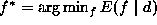 is not completely defined if the parameters are not specified even
if the functional form is known. These parameters must be specified or
estimated by some means. This is an important area of study in the MRF
vision modeling.
is not completely defined if the parameters are not specified even
if the functional form is known. These parameters must be specified or
estimated by some means. This is an important area of study in the MRF
vision modeling.
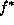 corresponds to the correct one? Before answering
this, let us make some remarks on the question. First, ``the minimal
solution''
corresponds to the correct one? Before answering
this, let us make some remarks on the question. First, ``the minimal
solution'' 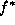 is meant to be the global one, or a global one if there
are multiple global minima. Second, ``the correct solution'', denoted
is meant to be the global one, or a global one if there
are multiple global minima. Second, ``the correct solution'', denoted
 , is said here in the subjective sense of our own
perception. For example, in edge detection, we run a program and get an
edge map as a solution; but we find that some edges are missing and some
false edges appear. This is the case where the solution differs from the
subjectively correct solution of ours.
, is said here in the subjective sense of our own
perception. For example, in edge detection, we run a program and get an
edge map as a solution; but we find that some edges are missing and some
false edges appear. This is the case where the solution differs from the
subjectively correct solution of ours.
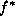 should
correspond to the correct solution
should
correspond to the correct solution 


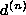 (
(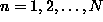 ).
Supposing that
).
Supposing that 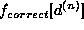 is the correct solution for
is the correct solution for
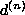 in our perception, we say that the functional form of the
energy E and the chosen parameters
in our perception, we say that the functional form of the
energy E and the chosen parameters 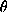 are correct for the N
observations if the following
are correct for the N
observations if the following
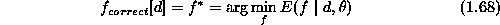
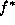 is the energy minimum, holds for each
is the energy minimum, holds for each 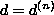 . Let
. Let
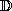 be the space of all possible observations. If
Eq.(
be the space of all possible observations. If
Eq.(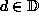 , we say that
E and
, we say that
E and  , hence the formulation, is entirely correct.
, hence the formulation, is entirely correct.
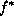 and the correct solution
and the correct solution  . Ideally, it should
be zero.
. Ideally, it should
be zero.
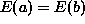 , as in Fig.
, as in Fig.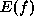 . The improvement is made by
adjusting either the functional form or the parameters so that the
improved energy function embeds the better solution as its unique
global minimum.
. The improvement is made by
adjusting either the functional form or the parameters so that the
improved energy function embeds the better solution as its unique
global minimum.