



Next: Low Level MRF Models
Up: Bayes Labeling of MRFs
Previous: Regularization
1.5.4
The procedure of the MAP-MRF approach for solving computer vision problems
is summarized in the following:
- Pose a vision problem as one of labeling in categories LP1-LP4
and choose an appropriate MRF representation f.
- Derive the posterior energy to define the MAP solution to a
problem.
- Find the MAP solution.
The process of deriving the posterior energy is summarized as the
following four steps:
- Define a neighborhood system
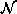 on
on 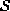 and the set of
cliques
and the set of
cliques  for
for 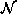 .
.
- Define the prior clique potentials
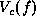 to give
to give 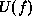 .
.
- Derive the likelihood energy
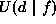 .
.
- Add
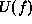 and
and 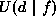 to yield the the posterior energy
to yield the the posterior energy
 .
.
The prior model depends on the type of the scene ( e.g.
the type of
surfaces) we expect. In vision, it is often one of the Gibbs models
introduced in Section 1.3. The likelihood
model depends on physical considerations such as the sensor process
(transformations, noise, etc.
). It is often assumed to be Gaussian. The
parameters in both models need be specified for the definitions of the
models to be complete. The specifications can be something of arts when
done manually and it is desirable that it is done automatically.
In the subsequent chapters, we are concerned with the following issues:
- Choosing an appropriate representation for the MRF labeling.
- Deriving the a posteriori distribution of the MRF as the
criterion function of the labeling solution. It mainly concerns the
specification of the forms of the prior and the likelihood
distributions. The involved parameters may or may not be specified at
this stage.
- Estimating involved parameters in the prior and the likelihood
distributions. The estimation is also based on some criterion, very
often, maximum likelihood. In the
unsupervised case, it is performed together with MAP labeling.
- Searching for the MRF configuration to maximize the posterior
distribution. This is mainly algorithmic. The main issues are the
quality (globalness) of the solution and the efficiency.
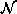 on
on 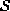 and the set of
cliques
and the set of
cliques  for
for 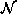 .
.
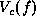 to give
to give 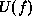 .
.
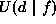 .
.
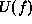 and
and 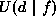 to yield the the posterior energy
to yield the the posterior energy
 .
.
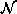 on
on 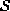 and the set of
cliques
and the set of
cliques  for
for 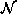 .
.
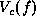 to give
to give 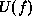 .
.
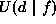 .
.
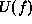 and
and 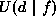 to yield the the posterior energy
to yield the the posterior energy
 .
.