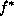1.5.1
In Bayes estimation, a risk is minimized to obtain the optimal estimate.
The Bayes risk of estimate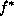 
is defined as
where d is the observation,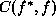 
is a cost function and 
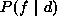is the posterior distribution. First of all, we need to compute
the posterior distribution from the prior and the likelihood. According
to the Bayes rule, the posterior probability can be computed by using
the following formulation
where 
is the prior probability of labelings f,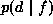 
is the conditional p.d.f. of the observations d, also called the
likelihood function of f for d fixed,
and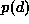 
is the density of d which is a constant when d is given.
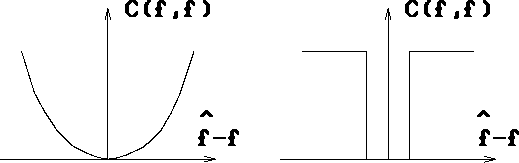
Figure 1.6: Two choices of cost functions.
The cost function 
determines the cost of estimate f when
the truth is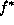 
. It is defined according to our preference. Two
popular choices are the quadratic cost function
where 
is a distance between a and b, and the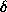 
(0-1) cost function
where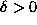 
is any small constant. A plot of the two cost
functions are shown in Fig.1.6.
The Bayes risk under the quadratic cost function measures the variance of the estimate
Letting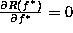 
, we obtain the minimal
variance estimate
The above is the mean of the posterior probability.
For the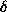 
cost function, the Bayes risk is
When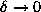 
, the above is approximated by
where 
is the volume of the space containing all points f for
which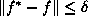 
. Minimizing the above is equivalent to
maximizing the posterior probability. Therefore, the minimal risk
estimate is
which is known as the MAP estimate. Because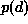 
in
(1.70) is a constant for a fixed d, 
is
proportional to the joint distribution
Then the MAP estimate is equivalently found by
Obviously, when the prior distribution,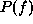 
, is flat, the MAP is
equivalent to the maximum likelihood.
