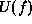1.3.3

The Smoothness Prior

A generic contextual constraint on this world is the smoothness.   It assumes that physical properties in a neighborhood of space or in an interval of time present some coherence and generally do not change abruptly. For example, the surface of a table is flat, a meadow presents a texture of grass, and a temporal event does not change abruptly over a short period of time. Indeed, we can always find regularities of a physical phenomenon with respect to certain properties. Since its early applications in vision [Grimson 1981; Horn and Schunck 1981; Ikeuchi and Horn 1981] aimed to impose constraints, in addition to those from the data, on the computation of image properties, the smoothness prior has been one of the most popular prior assumptions in low level vision. It has been developed into a general framework, called regularization [Poggio et al. 1985; Bertero et al. 1988], for a variety of low level vision problems.

Smoothness constraints are often expressed as the prior probability or equivalently an energy term 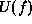measuring the extent to which the smoothness assumption is violated by f. There are two basic forms of such smoothness terms corresponding to situations with discrete and continuous labels, respectively.

The equations (1.52) and (1.54) of the MLL model with negative 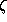and 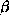coefficients provide a method for constructing smoothness terms for un-ordered, discrete labels. Whenever all labels 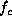on a clique c take the same value, which means the solution f is locally smooth on c, they incur a negative clique potential (cost); otherwise, if they are not all the same, they incur a positive potential. Such an MLL model tends to give a smooth solution which prefers uniform labels.

For spatially (and also temporally in image sequence analysis) continuous MRFs, the smoothness prior often involves derivatives. This is the case with the analytical regularization (to be introduced in Section 1.5.3). There, the potential at a point is in the form of . The order n determines the number of sites in the involved cliques; for example, 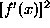where n=1 corresponds to a pair-site smoothness potential. Different orders implies different class of smoothness.

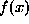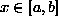Let us take continuous restoration or reconstruction of non-texture surfaces as an example. Let be the sampling of an underlying ``surface'' on where the surface is one-dimensional for simplicity. The Gibbs distribution 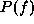, or equivalently the energy 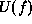, depends on the type of the surface f we expect to reconstruct. Assume that the surface is flat -- a priori. A flat surface which has equation should have zero first-order derivative, . 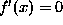Therefore, we may choose the prior energy as

which is called a string.   The energy takes the minimum value of zero only if f is absolutely flat or a positive value otherwise. Therefore, the surface which minimizes (1.56) alone has a constant height (grey value for an image).

In the discrete case where the surface is sampled at discrete points 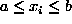, , 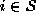we use the first order difference to approximate the first derivative and use a summation to approximate the integral; so the above energy becomes

where 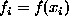. Expressed as the sum of clique potentials, we have

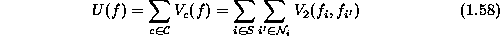
where 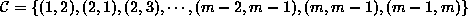consists of only pair-site cliques and

Its 2D equivalent is

and is called a membrane.  

Similarly, the prior energy 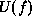can be designed for planar or quadratic surfaces. A planar surface, 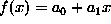, has zero second-order derivative, . Therefore, the following may be chosen

which is called a rod.   The surface which minimizes (1.61) alone has a constant gradient. In the discrete case, we use the second-order difference to approximate the second-order derivative and the above energy becomes

For a quadratic surface, 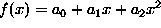, the third-order derivative is zero, 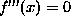and the prior energy may be

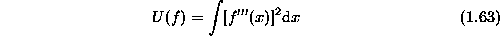
The surface which minimizes the above energy alone has a constant curvature. In the discrete case, we use the third-order difference to approximate the second-order derivative and the above energy becomes

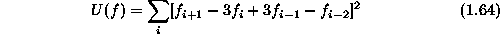
The above smoothness models can be extended to 2D. For example, the 2D equivalent of the rod, called a plate  , comes in two varieties, the quadratic variation

and the squared Laplacian

The surface which minimizes one of the smoothness prior energy alone has either a constant grey level, a constant gradient or a constant curvature. This is undesirable because constraints from other sources such as the data are not used. Therefore, a smoothness term 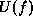is usually utilized in conjunction with other energy terms. In regularization, an energy consists of a smoothness term and a closeness term and the minimal solution is a compromise between the two constraints. Refer to Section 1.5.3.

The encodings of the smoothness prior in terms of derivatives usually lead to isotropic potential functions. This is due to the assumption that the underlying surface is non-textured. Anisotropic priors have to be used for texture patterns. This can be done, for example, by choosing (1.37) with direction-dependent 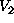's. This will be discussed in Section 2.4.